Flare-On 2024: fullspeed

fullspeed is a challenge around a .NET-AOT binary, which means unlike typical .NET binaries, it’s fully compiled to assembly. The binary makes an Elliptic Curve Diffie-Hellmen exchange and then uses it to send data including the flag. I’ll show how I use the given PCAP and the initialized values in the binary to recover the randomly generated privarte key, and decrypt the messages.
Challenge
The challenge prompt reads:
Has this all been far too easy? Where’s the math? Where’s the science? Where’s the, I don’t know…. cryptography? Well we don’t know about any of that, but here is a little .NET binary to chew on while you discuss career changes with your life coach.
The download contains an executable and a PCAP:
oxdf@hacky$ 7z l fullspeed.7z
...[snip]...
Date Time Attr Size Compressed Name
------------------- ----- ------------ ------------ ------------------------
2024-07-24 23:38:42 ....A 4660 1792 capture.pcapng
2024-07-24 02:49:14 ....A 2031616 769696 fullspeed.exe
------------------- ----- ------------ ------------ ------------------------
2024-07-24 23:38:42 2036276 771488 2 files
oxdf@hacky$ file fullspeed.exe
fullspeed.exe: PE32+ executable (console) x86-64, for MS Windows, 8 sections
oxdf@hacky$ file capture.pcapng
capture.pcapng: pcapng capture file - version 1.0
Running the binary, nothing obvious happens.
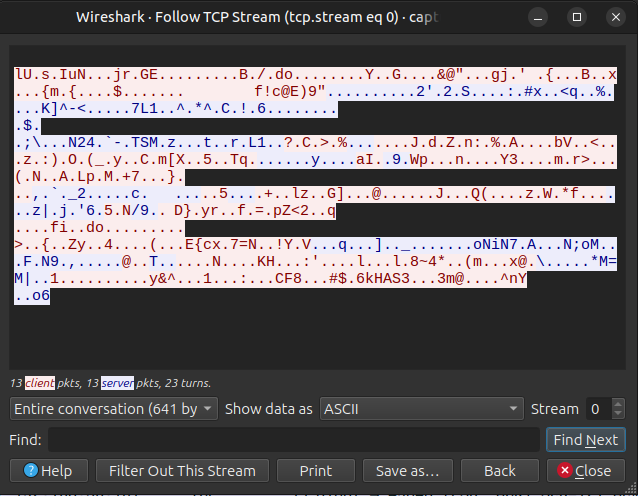
capture.png
The capture.png file consists of 40 packets between two hosts, 192.168.56.101 and 192.168.56.103. The stream looks like encrypted junk:
.NET AOT Application
Background
Typically when thinking of .NET binaries, they are made with C# (or F# or VB) code, which is compiled to Microsoft Intermediate Language (MSIL), which is then passed to the Common Language Runtime on the host at execution and compiled with “just in time” or JIT as it’s run to assembly which is executed by the processor.
It is possible to compile .NET with AOT (ahead of time) compilation to go directly from the source to assembly.
Identify
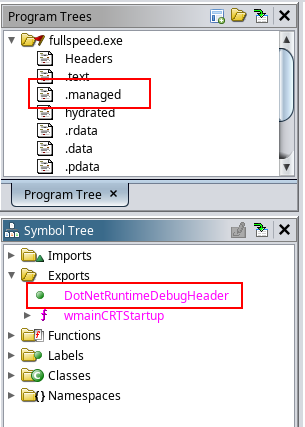
This post from Harfang Lab has nice background, including how to identify an AOT .NET binary:

Opening fullspeed.exe in Ghidra, I’ll see these:
Versions and Dependencies
Strings in the binary show the .NET version as 8.0.5:
oxdf@hacky$ strings fullspeed.exe | grep -i microsoft
*Microsoft Corporation
Microsoft Corporation. All rights reserved.
8.0.524.21615\8.0.5+087e15321bb712ef6fe8b0ba6f8bd12facf92629 Microsoft
Microsoft{I
Microsoft.Extensions.DependencyInjection.VerifyOpenGenericServiceTrimmability
<assembly xmlns="urn:schemas-microsoft-com:asm.v1" manifestVersion="1.0">
<trustInfo xmlns="urn:schemas-microsoft-com:asm.v2">
<requestedPrivileges xmlns="urn:schemas-microsoft-com:asm.v3">
They also show that it uses the BouncyCastle library:
oxdf@hacky$ strings fullspeed.exe | grep Bouncy
42BouncyCastle.Cryptography
:BouncyCastle.Cryptography.dll,System.Private.CoreLib
k@Legion of the Bouncy Castle Inc.9lml
Legion of the Bouncy Castle Inc. 2000-2024
mvBouncyCastle.NET is a popular cryptography library for .NET=nqn BouncyCastle.NET
oLBouncyCastle.NET Cryptography (net6.0)
BouncyCastle{
Identify Library Functions [Fail]
In theory now, the next step is to build signatures for the library functions. Over 95% of the binary is functions from the core .NET binaries and libraries. If I don’t have a strategy to identify them, then I’ll never make it through the entire binary to figure out what’s happening.
The post above has a way to generate a model binary with the appropriate .NET version and any libraries and use that to generate symbols based on them. Unfortunately, this process relies on paid IDA, which I do not have. I spent a good while trying different open source solutions from GitHub, and had some success getting some signatures loading into Ghidra, but also in the end, I had to get a FLIRT Signature file from a friend with paid IDA.
Update: This really nice post from washi shows how to map the function names over from a model Hello World binary to this one, and it’s awesome.
Break ECDH
ECDH Background
The binary performs an Elliptic-Curve Diffie-Hellman (ECDH) key establishment. In this, each partner has their shared base point (G), as well as their private key. Each multiplies the point by their key, and sends that to the other. They can each then multiply the received point by their private key, and that means that both have the same shared value, but an attacker in the middle observing the traffic can’t determine either private key. There’s an awesome diagram for this from elikaski’s ECC Attacks page:
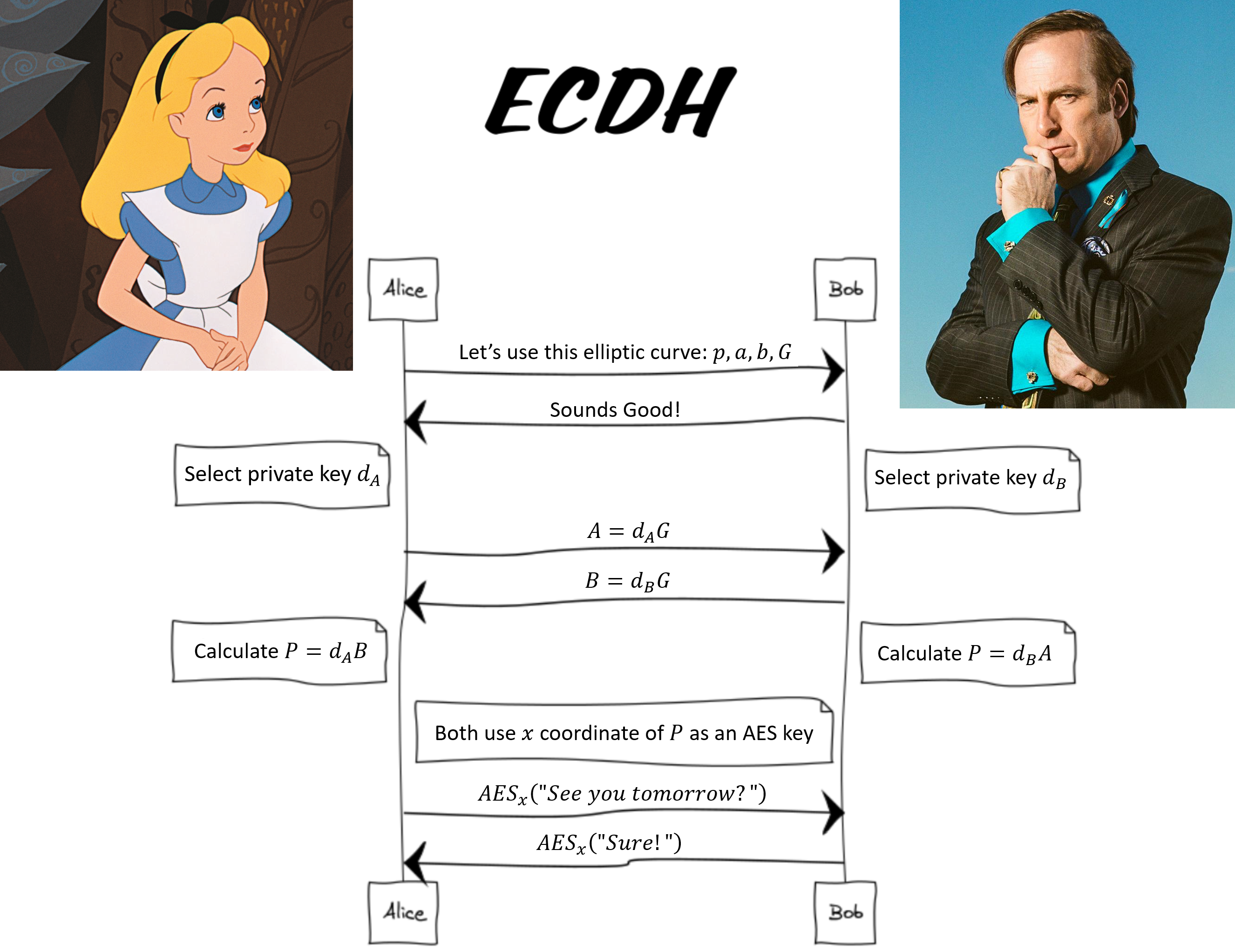
I found this image after completing this writeup, so I use x where the diagram uses dA.
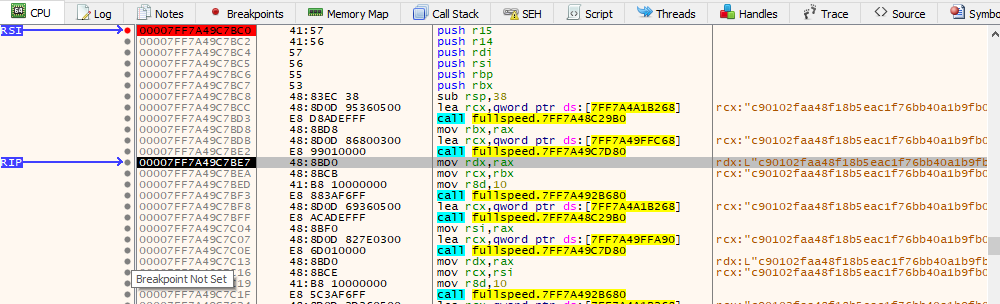
Initialization
In FUN_140107bc0, the binary initializes the ECDH. Each time it loads an obfuscated string from a global and deobfuscates it. For example, the first is q, which is a hex value starting with c90102faa48f18b5. On a couple steps, that value is presents in RCX:
Stepping through I can get the following constants:
q = int("c90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd", 16)
a = int("a079db08ea2470350c182487b50f7707dd46a58a1d160ff79297dcc9bfad6cfc96a81c4a97564118a40331fe0fc1327f", 16)
b = int("9f939c02a7bd7fc263a4cce416f4c575f28d0c1315c4f0c282fca6709a5f9f7f9c251c9eede9eb1baa31602167fa5380", 16)
Gx = int("087b5fe3ae6dcfb0e074b40f6208c8f6de4f4f0679d6933796d3b9bd659704fb85452f041fff14cf0e9aa7e45544f9d8", 16)
Gy = int("127425c1d330ed537663e87459eaa1b1b53edfe305f6a79b184b3180033aab190eb9aa003e02e9dbf6d593c5e3b08182", 16)
Communication
In FUN_140107ea0, the code generates a private key, a random 16 byte integer from the function call FUN_140107e20(0x80).
The point is then raised to the private key, and then xored by 48 bytes of 0x1337, and sent over the wire. It then gets back the points from the other host, and xors it by 48 bytes of 0x1337, and then raises it by it’s private key. Now it has successfully generated the shared secret between the two hosts.
In the PCAP, switching to raw view, it looks like:
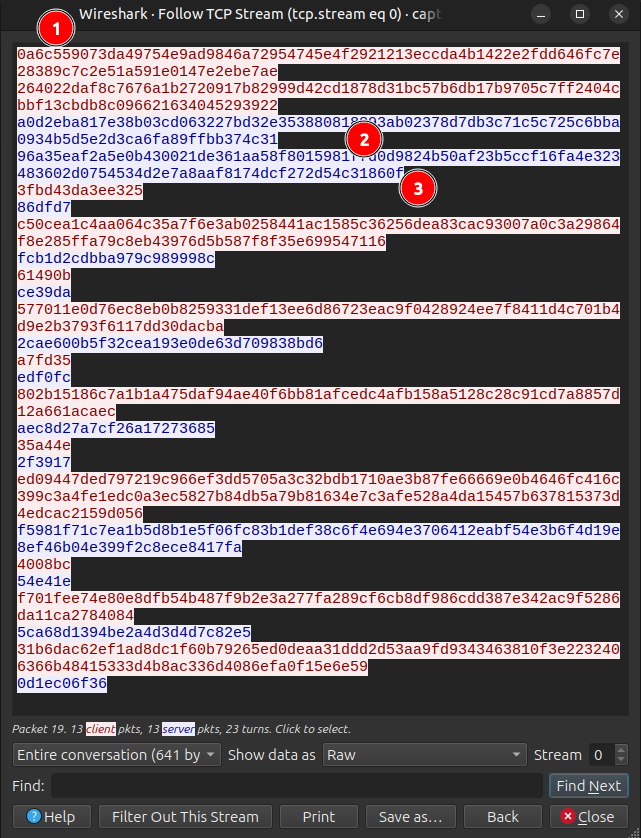
The two points sent at [1] are from one host, then the other two points at [2] are the others (noting there’s some extra data at the end [3]).
I’ll collect both the points sent by both parties, as I’ll need them each eventually.
Pohlig-Hellman
Recover x (Private Key)
The Pohlig-Hellman algorithm is an attack that I can use in a situation like this if the crypto is using weak curves. With a lot of help from ChatGTP, I’ll get Python code to use (using sage math) it to recover part of the secret key.
First I’ll get the points sent by the client from the first two lines of the raw PCAP stream:
leetkey = 0x133713371337133713371337133713371337133713371337133713371337133713371337133713371337133713371337
Px = 0x0a6c559073da49754e9ad9846a72954745e4f2921213eccda4b1422e2fdd646fc7e28389c7c2e51a591e0147e2ebe7ae ^ leetkey # first sent xored
Py = 0x264022daf8c7676a1b2720917b82999d42cd1878d31bc57b6db17b9705c7ff2404cbbf13cbdb8c096621634045293922 ^ leetkey # second sent xored
I’ll create an elliptic curve and two points on that curve:
E = EllipticCurve(GF(q), [a, b])
G = E(Gx, Gy)
P = E(Px, Py)
G is the starting point, and P is the point the client sent to the other host, which means it’s \(G \times x = P\).
I’ll get the order of the curve, and get it’s factors:
n = E.order()
print(f"order (n): {n}")
all_factors = [f[0] for f in factor(n)]
print("Factorization of n:", all_factors)
factors = [f for f in all_factors if f < 100000000]
Running to this point gives the factors of the order:
oxdf@hacky$ sage -python crack_ecdh.py
order (n): 30937339651019945892244794266256713890440922455872051984762505561763526780311616863989511376879697740787911484829297
Factorization of n: [35809, 46027, 56369, 57301, 65063, 111659, 113111, 7072010737074051173701300310820071551428959987622994965153676442076542799542912293]
Now I’ll factor using logs and CRT to recover a partial private key:
dl = []
for prime in factors:
Gi = G * (int(n)//prime)
Pi = P * (int(n)//prime)
d_log = discrete_log(Pi, Gi, operation="+")
dl.append(d_log)
print(f"log values: {dl}")
partial_k = int(crt(dl, factors))
print("Recovered partial private key:", partial_k)
This works:
oxdf@hacky$ sage -python crack_ecdh.py
order (n): 30937339651019945892244794266256713890440922455872051984762505561763526780311616863989511376879697740787911484829297
Factorization of n: [35809, 46027, 56369, 57301, 65063, 111659, 113111, 7072010737074051173701300310820071551428959987622994965153676442076542799542912293]
log values: [11872, 42485, 12334, 45941, 27946, 43080, 57712]
Recovered partial private key: 3914004671535485983675163411331184
Now that I have a partial x, I’ll brute force the rest of the bits, checking if \(G \times x = P\):
for i in range(2**16):
x = crt([partial_k, i], [int(prod(factors)), int(2**16)])
if x*G == P:
print(f"Private key: {x}")
print(f" {hex(x)}")
break
This returns the actual random number generated in the run that produced the PCAP:
oxdf@hacky$ sage -python crack_ecdh.py
order (n): 30937339651019945892244794266256713890440922455872051984762505561763526780311616863989511376879697740787911484829297
Factorization of n: [35809, 46027, 56369, 57301, 65063, 111659, 113111, 7072010737074051173701300310820071551428959987622994965153676442076542799542912293]
log values: [11872, 42485, 12334, 45941, 27946, 43080, 57712]
Recovered partial private key: 3914004671535485983675163411331184
Private key: 168606034648973740214207039875253762473
0x7ed85751e7131b5eaf5592718bef79a9
Recover Symmetric Key
To use that key, I need to get the point from the other host and multiple it by the private key:
Sx = 0xa0d2eba817e38b03cd063227bd32e353880818893ab02378d7db3c71c5c725c6bba0934b5d5e2d3ca6fa89ffbb374c31 ^ leetkey
Sy = 0x96a35eaf2a5e0b430021de361aa58f8015981ffd0d9824b50af23b5ccf16fa4e323483602d0754534d2e7a8aaf8174dc ^ leetkey
S = E(Sx, Sy)
private_point = x * S
Then I take the SHA512 of the x coordinate of that point, where the first 32 bytes are used as the key, and the next 8 as the nonce:
import hashlib
x_bytes = bytes.fromhex(hex(private_point[0])[2:])
hash_value = hashlib.sha512(x_bytes).hexdigest()
print(f"key: {hash_value[:64]}")
print(f"nonce: {hash_value[64:80]}")
The resulting run the keys:
oxdf@hacky$ sage -python crack_ecdh.py
order (n): 30937339651019945892244794266256713890440922455872051984762505561763526780311616863989511376879697740787911484829297
Factorization of n: [35809, 46027, 56369, 57301, 65063, 111659, 113111, 7072010737074051173701300310820071551428959987622994965153676442076542799542912293]
log values: [11872, 42485, 12334, 45941, 27946, 43080, 57712]
Recovered partial private key: 3914004671535485983675163411331184
Private key: 168606034648973740214207039875253762473
0x7ed85751e7131b5eaf5592718bef79a9
key: b48f8fa4c856d496acdecd16d9c94cc6b01aa1c0065b023be97afdd12156f3dc
nonce: 3fd480978485d818
Decrypt Traffic
I’ll go to CyberChef and set up to decrypt with ChaCha, entering the key and nonce from above. I’ll give it input from the data immediately following the points in the PCAP:
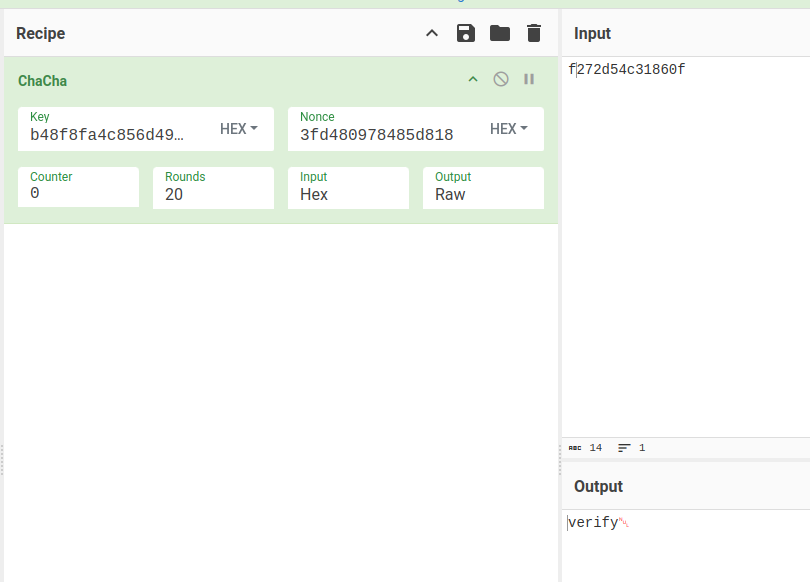
It decrypted to “verify\n”!
I’ll grab the rest of the data from the PCAP:
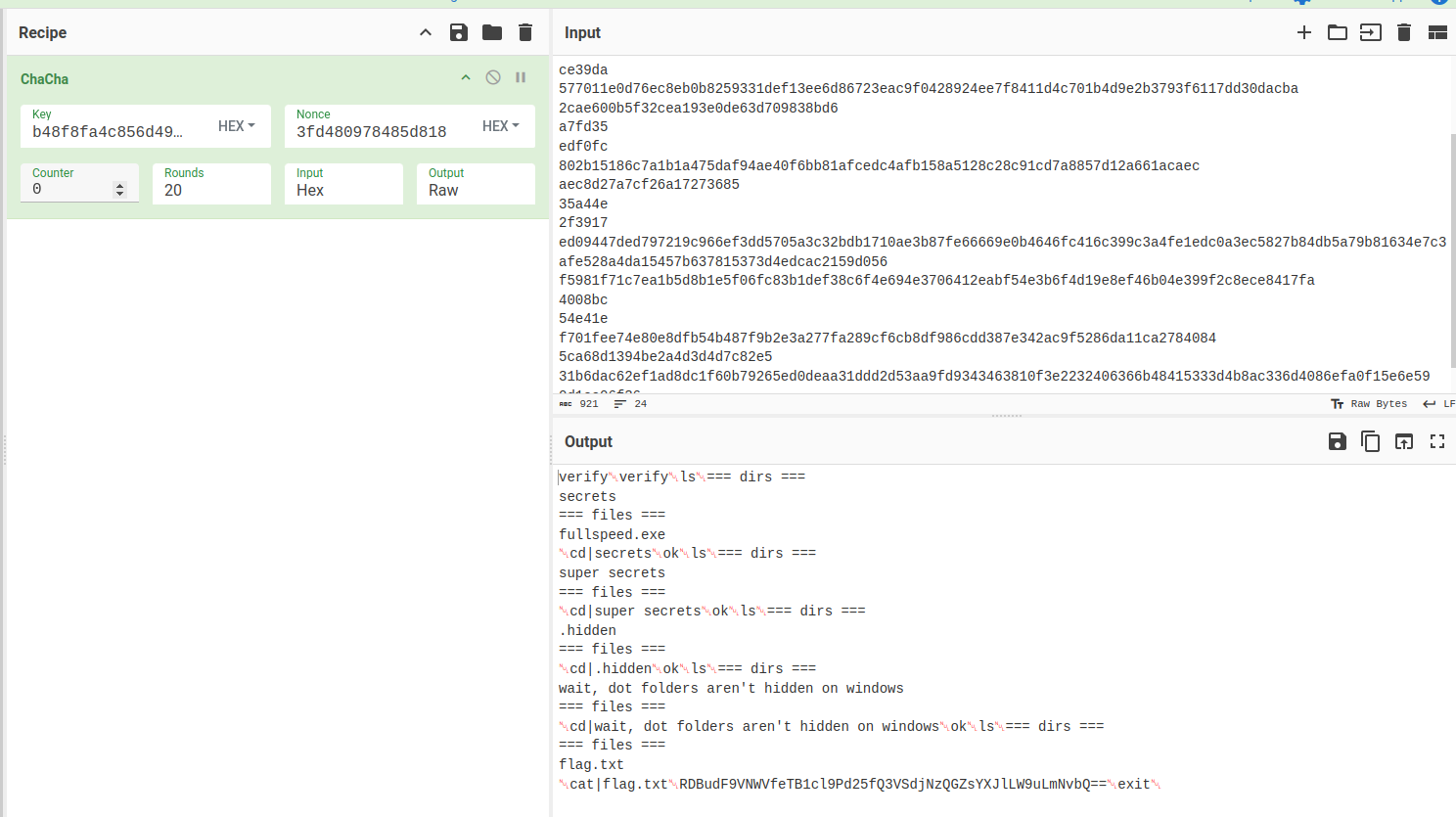
The last line is cat|flag.txt, and the result is a base64-encoded blob. I’ll decode it:
oxdf@hacky$ echo "RDBudF9VNWVfeTB1cl9Pd25fQ3VSdjNzQGZsYXJlLW9uLmNvbQ==" | base64 -d
D0nt_U5e_y0ur_Own_CuRv3s@flare-on.com