Flare-On 2022: encryptor

The given binary for encryptor is a fake ransomware sample. I’ll figure out which files it tries to encrypt, and then understand how it generates a random key for ChaCha20, then encrypts that key using RSA and attaches it. The mistake it makes is using the private key to encrypt, which means I can use the public key to decrypt, and get the ChaCha key, and then use that to decrypt a given file.
Challenge
You’re really crushing it to get this far. This is probably the end for you. Better luck next year!
The download contains a 64-bit stripped Windows executable:
oxdf@hacky$ file flareon.exe
flareon.exe: PE32+ executable (console) x86-64 (stripped to external PDB), for MS Windows
There’s also a file, SuspiciousFile.txt.Encrypted:
oxdf@hacky$ wc SuspiciousFile.txt.Encrypted
4 5 1101 SuspiciousFile.txt.Encrypted
oxdf@hacky$ file SuspiciousFile.txt.Encrypted
SuspiciousFile.txt.Encrypted: data
It starts with binary data, but then it switches to ASCII hex characters with a few newlines:
oxdf@hacky$ xxd SuspiciousFile.txt.Encrypted
00000000: 7f8a fa63 659c 5ef6 9eb9 c3dc 13e8 b231 ...ce.^........1
00000010: 3a8f e36d 9486 3421 462b 6fe8 ad30 8d2a :..m..4!F+o..0.*
00000020: 79e8 ea7b 6609 d8d0 5802 3d97 146b f2aa y..{f...X.=..k..
00000030: 6085 0648 4d97 0e71 ea82 0635 ba4b fc51 `..HM..q...5.K.Q
00000040: 8f06 e4ad 692b e625 5b39 6631 3837 3736 ....i+.%[9f18776
00000050: 6264 3365 3738 3833 3562 3565 6132 3432 bd3e78835b5ea242
...[snip]...
00000140: 6162 6132 6638 3261 310a 6463 3432 3563 aba2f82a1.dc425c
00000150: 3732 3034 3030 6530 3561 3932 6565 6236 720400e05a92eeb6
...[snip]...
00000230: 6263 3636 3966 3731 6562 3630 3937 6537 bc669f71eb6097e7
00000240: 3763 3138 3862 3962 6339 0a38 6536 3738 7c188b9bc9.8e678
00000250: 6630 3433 6330 6438 6238 6433 6466 6633 f043c0d8b8d3dff3
...[snip]...
00000330: 3235 6266 3463 3161 3033 3733 3464 3161 25bf4c1a03734d1a
00000340: 3762 3064 6664 6366 6434 340a 3561 3034 7b0dfdcfd44.5a04
00000350: 6539 3563 6430 6539 6266 3063 3863 6464 e95cd0e9bf0c8cdd
...[snip]...
00000430: 3734 6439 3734 6631 3335 6162 3166 3438 74d974f135ab1f48
00000440: 3939 3934 3634 3238 3138 3463 0a 99946428184c.
Getting It To Encrypt
Initial Run
Double clicking on flareon.exe doesn’t do anything, suggesting it exits without opening a window. Running it from a terminal shows it’s printing a usage:
PS > .\flareon.exe
usage: flareon path [path ...]
I’ll try making a test directory and see if it will encrypt, but it doesn’t:
PS > mkdir test
Directory: Z:\flareon-2022\09-encryptor
Mode LastWriteTime Length Name
---- ------------- ------ ----
d----- 10/20/2022 10:27 AM test
PS > echo "hello" > .\test\test.txt
PS > cat .\test\test.txt
hello
PS > .\flareon.exe test
0 File(s) Encrypted
PS > .\flareon.exe .\test\test.txt
0 File(s) Encrypted
Finding File Extension
Finding main
I’ll load the binary into Ghidra and do the standard processing.
Looking at the strings, the “usage” string jumps out as an interesting place to start:
This leads to the bottom of FUN_403bf0:

The close } pairs back to an open on line 26:

Basically, if argc (the number arguments, counting the name of the running file) isn’t more than one, then it prints the usage and exits.
Loop
After the argc check, there’s a series of nested loops over the arguments:
If the arguments is null, it does some stuff and returns.
It then uses a loop to get the pointer 10 bytes from the end of the argument. If the argument isn’t that long, it loops.
Then it does a memcmp with “.EncryptMe” and the last 10 bytes of the input, and if they don’t match, or if the file can’t be opened, it loops.
So effectively, to continue beyond the blue loop, it must be a file that can be opened ending in .EncryptMe.
Encrypt File
I’ll create a test file, test.EncryptMe and pass it to flareon.exe:
PS > cat .\test.EncryptMe
This is a test file
PS > .\flareon.exe .\test.EncryptMe
.\test.EncryptMe
1 File(s) Encrypted
The file is still there and unchanged, but there’s a test.Encrypted file as well:
PS > cat .\test.Encrypted
óÐlD³ìIE↨Ê”XAÃ’CïE‘9f18776bd3e78835b5ea24259706d89cbe7b5a79010afb524609efada04d0d71170a83c853525888c942e0dd1988251dfdb3cd85e95ce22a5712fb5e235dc5b6ffa3316b54166c55dd842101b1d77a41fdcc08a43019c218a8f8274e8164be2e857680c2b11554b8d593c2f13af2704e85847f80a1fc01b9906e22baba2f82a1
ce347ce09e2e8ce374dd0d7928bfb41e54407e6a529642fe4940e1743e1d2473ad1facdb303ce2c2f34d7315ae4856727c1292c4093d8698ee7b311f2cbdc52065bddf3102b6b0df8d29883ef1316e54e30f03d657e9e0c65cc2eb0a1267b102c2426147d6be20a26932e35ecb8a1b06351ed2bfadd63abaf3d58be85cc44df9
82e50dd463706d4f5c5a9d06683a74e513c1f133777b29c584b3c105948414501b29d6bfd3393b4d783bbe94c771638096a874d8e2e8570caeeef20ad618981f63808f709d98a1729be7fb6bd5272781e51c31cdd1b59acf5cd02095663290f973f01811539a64b2ead7ca72f2e42a05eeb270361811f2112629049e0255cd29
6399b7f334a5d1b01620b64bd1d48a2decb7e34ce3e343952b9ab970a257950ed95fa01d76e45c2e4d47a69a0f32f2bfd45e8f6f98730ca3bc2465e0754c110840fe37c0c6dad8c435a6e87e7ff92b98f38b39c2e6a4de6deea998363bde71be9d5f448dcd049636d6d0d68d273da59730b0af3f7a6b26e39a51200a76def885
Encrypted Structure
The newly encrypted file has the same structure as the SuspiciousFile.txt.Encrypted file that came with the challenge.

There’s binary data at the front, and then four strings of ASCII hex data. Each hex string is followed by a newline. The hex editor view shows it nicely as well:
The binary data is 19 bytes long, which is the same length as the plaintext data from the original file. Another test on a file of a different size shows that the output data is composed of:
- binary data of length matching original data
- four 128 hex characters strings, each followed with a new line
RE
main
RtlGenRandom
I already looked at bit at main (0x403bf0), but there’s more to note there. The function starts off by getting a handle to the advapi32 library, and then using that to get the address of “SystemFunction036”:

This is the RtlGenRandom function, which according to the docs, is only for operating system use, and isn’t importable, but rather must be loaded with this resource name “SystemFunction036” from Advapi32.dll.
The address of this function is saved in a global variable for later use.
Initialize RSA
There’s one other functions to note in main. First, just after validating there’s at least one argument, it calls a function I’ve named initialized_rsa:

I’ll dig into this below.
Encrypt File
Earlier I noted that it would just loop back to the top if the argument didn’t end in .EncryptMe or if it couldn’t be opened. If it clears all these checks, it reaches the following:

It duplicates the filename and overwrites the extension with .Encrypted. It opens both files (ignore the bad decompile that makes it look like it overwrites the handle), and then passes both file handles into encrypt_file.
RSA
The initialize_rsa function (0x4021d0) creates the necessary primitives for RSA:

I don’t completely understand how each of the functions in here work, but once I got a feeling that this was RSA encryption (both from the structure of this function as well as how the globals that are stored are used later), I’ll take the approach of looking at what should happen and debugging to prove it.
For example, it starts with these while loops creating two large prime numbers, which I’ve named p and q. In RSA, it’ll multiply those two numbers together to make n. I’ll break at the call to mult_bigint, which takes these two numbers and a global:
I’ll copy that hexdump and throw it into CyberChef:

And from there into Python (and the same with q):
>>> p = int.from_bytes(b'\xdf\xa0\x60\xd0\x26\xe0\x93\xa4\x91\x3a\x85\xb7\x45\xa2\xb4\xda\xe5\x21\x14\x98\xc3\x4a\xcf\x71\xfb\x68\xbc\xa1\xab\x8c\xb7\xe5\x6f\xaf\xe5\x6b\x79\xad\xb5\x41\xe4\xe6\xd1\xfd\x83\x09\x70\xe8\x00\x68\x37\x94\x78\x24\x37\xe4\xc0\xca\xd6\x98\xec\x83\xe1\xd3', 'little')
>>> q = int.from_bytes(b'\x1f\xf5\x38\x80\xd8\x89\x6c\xd8\x81\x1e\xff\xd1\x8f\x96\x4d\xbd\x30\xe6\x54\x2a\xfd\x00\xd4\xca\xe4\x58\xfb\x3a\x9d\xd5\x0a\x1e\x40\xf8\x0e\x72\xcd\x35\xc7\x8b\x8a\x70\x2d\x4f\x8d\xb0\x03\x6b\x69\xaf\x47\xf4\x8c\x23\x68\xfc\x22\xe9\xb2\x81\xef\xa8\xbd\xcb', 'little')
I’ll point my dump at the global (0x409100), which is currently all nulls:

On stepping over the call to mult_bigint (0x401550), the buffer is updated:

Throwing that into Python, I’ll verify that function just multiplies the two inputs together and stores the output in the first arg:
>>> n = int.from_bytes(b'\x01\xe6\x70\x66\xda\x42\xce\x71\xb3\xf3\xec\x4c\x1c\x2b\x1f\xb7\xd8\x06\xbc\xc0\x93\x37\xac\x0c\xa7\x8c\x1c\xff\x59\x94\x10\x9a\xde\x59\x30\x7e\x9c\x21\xb0\xbe\x3f\xbc\x23\xe6\x1e\x05\x57\x50\xd4\x36\xd3\x4c\xa3\x70\x75\x6a\xa4\xac\x16\xef\x03\xd9\x4c\xb1\xe2\x16\x01\xfe\x78\x1b\x92\x92\xf2\x6b\x38\x62\x73\x52\x10\x40\x9f\x33\x32\xbc\xe7\xb0\x33\x9e\xe9\x52\x3e\x84\xfd\x86\x94\x5e\x79\x2b\x01\x8d\x67\xb5\x59\xa5\xa4\x32\x2c\xfe\xbb\x38\xc0\x8e\xdc\xca\x43\xbf\x6d\xa3\x6a\x74\xc7\x4e\x55\x3c\xed\xcc\xa0\xa8', 'little')
>>> n == p * q
True
In RSA, I’ll need to calculate Φ, which is p-1 * q-1. The next function subtracts one. The input buffer (top) is the same as the output (bottom), except the first byte is one less:

Next, the same mult_bigint function is called on p-1 and q-1, creating Φ. With n and Φ, the next step would be to pick an e, and use it to calculate d. The default e is typically 0x10001.
The next call confused me for a bit:
get_private_key((undefined4 *)&d,(undefined4 *)&d,phi);
Until I noticed that the global I named d (0x404020) is initialized to 0x10001, and then after this call it’s been updated.
There’s another line at the bottom where it calls what I’ll later determine is the RSA_encrypt_decrypt function on some other stuff, but I never dug into that deeply. It is using another global (0x405000) that’s initialized to 0x10001, suggesting it’s e.
Encrypt File
ChaCha20
The function I’ve named encrypt_file (0x4022a3) starts by nulling out two buffers, and then calling the RtlGenRandom function to put 0x20 bytes in the first, and 0xc bytes in the next:

The two file handles and the two random buffers are passed into another function. In that function, some constants jump out:

Googling for one returns results including the other, with references to the ChaCha20 encryption scheme:

ChaCha20 takes a 0x20 byte key and a 0xc byte nonce, which match the random buffers passed in. Without any additional RE, I’ll assume it’s using ChaCha20 to encrypt the input file using the random key and nonce, and the result is written to the output file.
RSA
The next function takes in the chachakey, d, and n, as well as a buffer that the results are written to. Without even looking at the function, it seems very likely that the binary is encrypting the ChaCha key (and nonce) using asymmetric crypto (RSA). This is a very common tactic in ransomware. Asymmetric crypto can be really slow. So when you want to encrypt a lot, it’s faster to generate a random key, use that to encrypt with something symmetric (like ChaCha20), then encrypt that with the public key, and store the encrypted symmetric key with the file. Only someone with the private key (which never has to touch the victim computer) can decrypt the symmetric key and then the file.

Write Outfile
The rest of this function is writing things to the file:

write_hex converts binary to hex, and then writes it. I don’t really know what the signature?? or DAT_00409060 are. But n and the encrypted_key_iv are both written into the file.
This accounts for the four hex buffers with newlines in the output.
Decrypt
Strategy
The encrypted file has the encrypted symmetric key (and nonce), as well as n as part of the public key.
There was a subtle mistake the “malware” author made here, which is using the private key to encrypt. There’s nothing special from the math side about the two keys. If you encrypt with one, you can decrypt with the other. In general, we encrypt with a public key, so that only someone with the private key can read it. But digital signatures are based on the same concept, but using the private key to sign, allowing anyone to verify with the public key.
Had the authors done this correctly and encrypted with the public key (n and e) instead of the private (n and d), there’s no way I could recover the file. But because they used d to encrypt, that means I only need to know n and e to decrypt. e is hard coded as 0x10001, and n is in the file.
Script
I’ll write a Python script to read the file and generate the plaintext. This video shows the process:
The resulting script is:
#!/usr/bin/env python3
import sys
from Crypto.Cipher import ChaCha20
with open(sys.argv[1], 'rb') as f:
encfile = f.read()
values = encfile.rsplit(b'\n', 4)
enc_key_nonce = int(values[3], 16)
n = int(values[1], 16)
ct = values[0][:-256]
pt_key_nonce = pow(enc_key_nonce, 0x10001, n).to_bytes(48, 'little')
chachakey = pt_key_nonce[:32]
chachanonce = pt_key_nonce[-12:]
chacha = ChaCha20.new(key=chachakey, nonce=chachanonce)
pt = chacha.decrypt(ct)
print(pt.decode())
It reads the file and uses rsplit to split four times from the end, allowing there to be additional newlines in the encrypted data. Then it gets the encrypted ChaCha secrets, n, and the cipher text. It uses n to decrypt the secrets, and then uses them to decrypt the flag message.
It gets the flag:
oxdf@hacky$ python decrypt.py SuspiciousFile.txt.Encrypted
Hello!
The flag is:
R$A_$16n1n6_15_0pp0$17e_0f_3ncryp710n@flare-on.com
Flag: R$A_$16n1n6_15_0pp0$17e_0f_3ncryp710n@flare-on.com
 Click for full size image
Click for full size image Click for full size image
Click for full size image Click for full size image
Click for full size image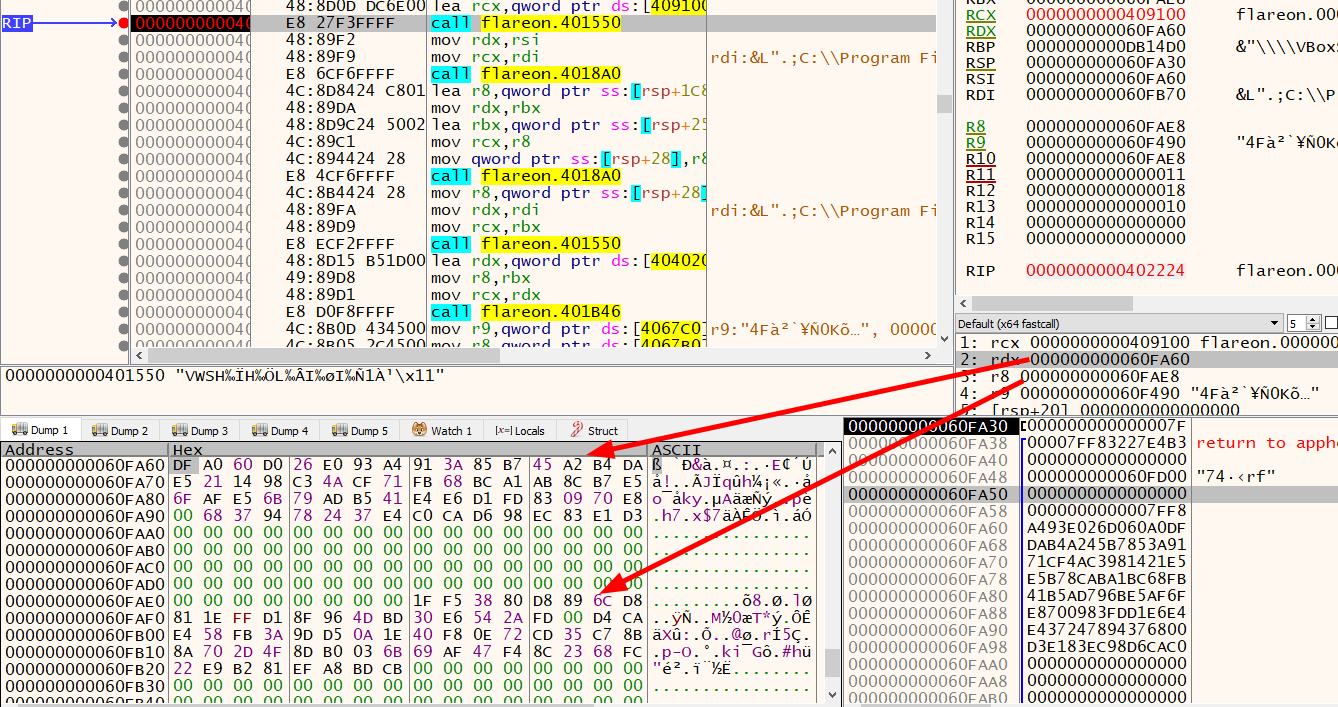 Click for full size image
Click for full size image